GÉOMÉTRIE ALGÉBRIQUE

GÉOMÉTRIE ALGÉBRIQUE

Sous sa forme actuelle, la géométrie algébrique est une branche de l’algèbre relativement récente (cf. ALGÈBRE, DEDEKIND). Pour «comprendre» les phénomènes d’intersection des courbes et des surfaces, il s’est révélé nécessaire d’élaborer des techniques compliquées qui se sont développées de manière abstraite et sont venues à leur tour enrichir d’autres domaines des mathématiques (théorie moderne des nombres, fonctions analytiques de plusieurs variables complexes, topologie algébrique); pour le profane, cet appareil mathématique peut sembler bien loin de l’«intuition géométrique»!

La géométrie algébrique est issue de l’étude des courbes algébriques du plan R² ou de l’espace R³ et des surfaces algébriques de R³. Pendant le XVIII^e et le XIX^e siècle, on s’est aperçu qu’il était plus commode de modifier le problème en se plaçant dans le plan complexe C² ou dans l’espace complexe C³; en effet, C est un corps algébriquement clos, de sorte que les courbes et les surfaces ont toujours «suffisamment» de points à coordonnées complexes, alors qu’il peut n’y avoir aucun point à coordonnées réelles (comme c’est le cas pour la courbe d’équation x ² + y ² + 1 = 0). On a observé aussi que certains énoncés intéressants n’étaient vrais que si l’on complétait les courbes et les surfaces par des «points à l’infini», se plaçant ainsi dans le plan projectif P²(C) ou dans l’espace projectif P³(C); les courbes ou les surfaces y sont définies par des équations polynomiales homogènes portant sur les coordonnées homogènes ^{[cf. COURBES ALGÉBRIQUES]}.

Cette diversité de points de vue (réel ou complexe, affine ou projectif) a dû être encore élargie lorsque la théorie des nombres a mis en évidence l’intérêt de l’étude des courbes algébriques définies sur des corps autres que R ou C, comme les corps finis ou les corps p -adiques; la théorie des équations diophantiennes conduit même à considérer des courbes ou des ensembles algébriques définis sur un anneau tel que Z. Pendant la première moitié du XX^e siècle, l’école allemande a développé la théorie des ensembles algébriques (de dimension quelconque) de l’espace affine k ⁿ ou de l’espace projectif Pⁿ (k ), k étant un corps de base algébriquement clos arbitraire.

Pour l’étude des propriétés intrinsèques d’un ensemble algébrique, il est plutôt gênant d’avoir à le considérer comme plongé dans un espace affine ou un espace projectif. Le problème se pose donc de définir des «variétés algébriques abstraites», non plongées dans k ⁿ ou Pⁿ (k ), un peu comme on définit des variétés différentiables indépendamment d’un plongement dans Rⁿ en géométrie différentielle ^{[cf. VARIÉTÉS DIFFÉRENTIABLES]}. De telles variétés abstraites ont été définies par A. Weil (1946). Une définition équivalente, plus simple et plus maniable se trouve dans l’article de J.-P. Serre, «Faisceaux algébriques cohérents» (1955); elle est inspirée de la théorie des espaces analytiques. Dans le présent article, nous donnerons la définition de Serre un peu élargie, en prenant comme corps de base un corps algébriquement clos. Le cas d’un corps de base non algébriquement clos, ou d’une base plus générale, s’exprime bien dans le cadre de la théorie des schémas de A. Grothendieck, qui généralise considérablement celle des variétés algébriques au sens de Serre en partant du même point de vue.

1. Ensembles algébriques

Soit k un corps de base algébriquement clos. Pour tout entier naturel n , l’espace affine k ⁿ est l’ensemble des suites (x ¹, x ², ..., x ⁿ ) de n éléments de k ; on appelle ces n éléments les coordonnées du point x = (x ¹, x ², ..., x ⁿ ) de k ⁿ . L’espace projectif Pⁿ (k ) est le quotient de k ⁿ⁺¹ 漣O, complémentaire de l’origine O = (0, 0, ..., 0), par la relation d’équivalence qui identifie (x ⁰, x ¹, ..., x ⁿ ) à toute suite proportionnelle (tx ⁰, tx ¹, ..., tx ⁿ ) (t élément non nul de k ); on voit que les points Pⁿ (k ) sont les droites passant par O dans k ^{n + 1} , privées de O. Si un élément (x ⁰, x ¹ ..., x ⁿ ) de k ^{n + 1} représente un point x de Pⁿ (k ), on dit que les coordonnées x ⁰, x ¹, ..., x ⁿ de cet élément sont des coordonnées homogènes de x ; elles ne sont pas toutes nulles et sont définies à un facteur de proportionnalité près.

Une partie X de k ⁿ est un ensemble algébrique affine si c’est l’ensemble des zéros communs à des polynômes f ¹, f ², ..., f ^s par rapport aux coordonnées; on dit que X est défini par les équations:

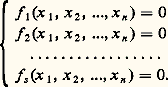Un ensemble algébrique projectif dans Pⁿ (k ) est défini d’une manière analogue par des équations polynomiales homogènes par rapport aux coordonnées homogènes.

Applications régulières

Soient X 說 k ^m et Y 說 k ⁿ des ensembles algébriques affines; une application u de X dans Y est dite régulière si les coordonnées u ¹(x ), u ²(x ), ..., u ⁿ (x ) de u (x ) sont des fonctions polynomiales des coordonnées du point x de X. En particulier, les applications régulières de X dans k , encore appelées fonctions régulières sur X, sont les fonctions polynomiales des coordonnées d’un point de X; elles forment un sous-anneau de l’anneau de toutes les applications de X dans k , et ce sous-anneau est visiblement isomorphe au quotient de l’anneau des polynômes k [¹, ², ..., Tⁿ ] par l’idéal des polynômes qui s’annulent sur X.

Il est clair que la composée de deux applications régulières est une application régulière. En particulier, une application régulière u : XY définit un homomorphisme f 料 f 獵 u , de l’anneau des fonctions régulières sur Y dans l’anneau des fonctions régulières sur X. Un isomorphisme d’un ensemble algébrique X sur un autre Y est une application bijective de X sur Y, qui est régulière ainsi que sa réciproque; il définit un isomorphisme de l’anneau des fonctions régulières sur Y sur l’anneau des fonctions régulières sur X.

On trouvera ci-après quelques exemples d’applications régulières.

– Paramétrisation d’une parabole (fig. 1). Considérons l’application u de la droite k dans le plan k ² définie par u (t ) = (t , t ²). L’image u (k ) est la parabole X d’équation y = x ², et u définit une bijection de k sur X, réciproque de l’application (x , y ) 料 x ; on a donc un isomorphisme de la droite k sur la parabole X.

– Cissoïde (fig. 2). L’application v : t 料 (t ², t ³) de k dans k ² est aussi une application régulière. Elle applique la droite k bijectivement sur son image, qui est la «parabole semi-cubique» (ou cissoïde) Y d’équation y ² = x ³; mais ce n’est pas un isomorphisme de k sur Y, car la bijection réciproque v , définie par v (x , y ) = y /x si x 0 et v (0, 0) = 0 n’est pas une application régulière. En fait on peut montrer que la cissoïde Y n’est pas isomorphe à une droite en observant que son anneau de fonctions régulières n’est pas intégralement clos (la fraction z = y /x vérifie l’équation z ² = x , donc est entière sur cet anneau, sans y appartenir, cf. ANNEAUX COMMUTATIFS), et ne peut par suite être isomorphe à l’anneau k [T] des fonctions régulières sur k.

– Paraboloïde (fig. 3). L’application rationnelle (x , y ) 料 (x , y , xy ) du plan k ² dans l’espace k ³ définit un isomorphisme du plan sur le paraboloïde d’équation z = xy.

Pour définir les applications régulières d’un ensemble algébrique projectif X 說 P^m (k ) dans un autre Y 說 Pⁿ (k ), on procède de la même façon. Une application u de X dans Y est régulière si les coordonnées homogènes de u (x ) peuvent s’exprimer par des polynômes homogènes u ⁰, u ¹, ..., u ⁿ , tous de même degré par rapport aux coordonnées homogènes de x ; notons que ces polynômes ne peuvent s’annuler simultanément pour x 捻 X. Si maintenant X 說 k ^m est affine et Y 說 Pⁿ (k ) est projectif, les applications régulières de X dans Y sont définies en donnant les coordonnées homogènes sur Y comme fonctions polynomiales (ne s’annulant pas simultanément) des coordonnées sur X; quant aux applications régulières de Y dans X, ce sont les applications constantes (les polynômes homogènes de degré 0 sont les seuls à être constants sur chaque droite issue de l’origine dans k ⁿ⁺¹ ).

Par exemple, l’application 見ⁿ de k ⁿ dans Pⁿ (k ) qui transforme (x ¹, x ², ..., x ⁿ ) en le point de coordonnées homogènes (1, x ¹, ..., x ⁿ ) est régulière; elle définit une bijection de k ⁿ sur le complémentaire de l’hyperplan d’équation homogène x ⁰ = 0 dans Pⁿ (k ) (fig. 4). Tout ensemble algébrique X de k ⁿ s’identifie par 見ⁿ à la partie d’un ensemble algébrique X de Pⁿ (k ) où x ⁰ 0; si les équations de X sont :

les équations homogènes de X sont:

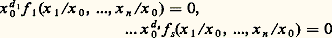(d ⁱ désigne le degré f ⁱ ); nous dirons que X est la complétion projective de X. Toute application régulière u d’un ensemble algébrique affine X dans un autre Y se prolonge d’une manière unique en une application régulière de X dans Y. En particulier, l’application u : t 料 (t , t ²) de k dans k ² se prolonge en l’application régulière : P¹(k ) 料 P²(k ), qui transforme le point de coordonnées homogènes (x , y ) en le point de coordonnées homogènes (x ², xy , y ²); cette application définit un isomorphisme de la droite projective P¹(k ) sur la conique X complétée de la parabole X (cf. exemple ci-dessus), dont l’équation homogène est y ² = xz .

On peut généraliser l’exemple précédent et l’on peut ainsi définir pour tout couple (n , d ) d’entiers naturels une application régulière de Pⁿ (k ) dans P^e (k ) dans laquelle e = (n + 1)(n + 2)... (n + d )/d! 漣 1, de manière à obtenir un isomorphisme de Pⁿ (k ) sur un ensemble algébrique V^n,d dans P^e (k ) (la variété de Veronese); les coordonnées homogènes du transformé de x sont tous les monômes de degré d par rapport aux coordonnées homogènes de x .

Applications rationnelles

En remplaçant les polynômes par des fractions rationnelles dans tout ce qui précède, on obtient des «applications» non partout définies en général (car les dénominateurs peuvent s’annuler; il y a donc un abus de langage à parler d’applications); ce sont les applications rationnelles. Nous ne donnons de définition précise que dans le cas des fonctions rationnelles (applications rationnelles à valeur dans k ). Considérons d’abord un ensemble algébrique affine X dans k ⁿ ; une fonction rationnelle f sur X est définie par une fraction P/Q 捻 k (T¹, ², ..., Tⁿ ), dont le dénominateur ne s’annule pas identiquement sur X; c’est l’application x 料 P(x )/Q(x ) de l’ensemble U =x 捻 X | Q(x ) 0 dans k. De même, pour définir une fonction rationnelle sur un ensemble algébrique projectif X 說 Pⁿ (k ) on prend une fraction P/Q en coordonnées homogènes, avec P et Q homogènes de même degré (pour avoir une fonction constante sur les droites issues de O dans k ⁿ⁺¹ ) et Q non identiquement nul sur X.

La composée de deux applications rationnelles f de X dans Y et g de Y dans Z peut se définir si l’ensemble des points x de X tels que f soit définie en x et g en f (x ) n’est contenu dans aucun ensemble algébrique strictement plus petit que X; c’est encore une application rationnelle. Une équivalence birationnelle entre X et Y est un couple (u , v ) où u est une application rationnelle de X dans Y et v une application rationnelle de Y dans X, les composés v 獵 u et u 獵 v étant les applications identiques de X et Y respectivement.

Par exemple (x , y ) 料 y /x est une fonction rationnelle dans le plan k ², définie dans le complémentaire de la droite d’équation x = 0. Sa restriction à la courbe d’équation y ² = x ³ est une fonction rationnelle définie en dehors de l’origine; on voit que la cissoïde est birationnellement équivalente à la droite (sans lui être isomorphe; cf. exemple supra et fig. 2). D’une manière générale, on dit qu’une courbe algébrique est unicursale si elle est birationnellement équivalente à la droite k (cf. COURBES ALGÉBRIQUES). Les fractions x ¹/x ⁰, x ²/x ⁰, ..., x ⁿ /x ⁰ définissent une application rationnelle de Pⁿ (k ) dans k ⁿ ; cette application est définie dans le complémentaire de l’hyperplan d’équation homogène x ⁰ = 0 et donne (avec 見ⁿ ; cf. supra ) une équivalence birationnelle entre Pⁿ (k ) et k ⁿ . De même, tout ensemble algébrique affine est birationnellement équivalent à sa complétion projective.

2. Variétés algébriques affines

À tout ensemble algébrique affine X 說 k ^m , nous avons associé la k -algèbre A(X) des fonctions régulières sur X; elle est isomorphe (d’une manière canonique) au quotient k [¹, ², ..., T^m ]/I(X) où I(X) désigne l’idéal formé des polynômes qui s’annulent sur X. Si une application u : XY d’un ensemble algébrique dans un autre est régulière, f 獵 u appartient à A(X) pour toute fonction f de A(Y). Inversement, cette condition implique que u est régulière; remplaçons en effet f par les fonctions coordonnées y ¹, y ², ..., y ⁿ de Y: nous obtenons des fonctions u ⁱ = y ⁱ 獵 u (i = 1, 2, ..., n ) régulières sur X, c’est-à-dire induites par des polynômes en les coordonnées de X.

On voit même que tout homomorphisme 﨏 de A(Y) dans A(X) détermine une application régulière u de X dans Y telle que 﨏 soit l’application f 料 f 獵 u ; les coordonnées de u sont les fonctions 﨏(y ¹), 﨏(y ²), ..., 﨏(y ⁿ ) de A(X). Considérons, en particulier, le cas où X =e est réduit à un point; c’est l’espace affine k ⁰ et son algèbre de fonctions régulières se réduit aux constantes A(X) = k . La donnée d’une application (régulière automatiquement) u : X =eY, c’est-à-dire d’un point y = u (e ) de Y, équivaut donc à celle de l’homomorphisme f 料 f 獵 u = f (y ) de A(Y) dans k ; d’où une bijection de l’ensemble Y sur l’ensemble Hom^k (A(Y), k ) des homomorphismes de A(Y) dans k.

Tout isomorphisme A(Y)A(X), où X et Y sont des ensembles algébriques affines, détermine un isomorphisme de X sur Y. Cela nous met sur la voie d’une définition intrinsèque des ensembles algébriques affines, indépendamment du plongement dans un espace k ⁿ : la structure d’ensemble algébrique est définie par la donnée de l’algèbre des fonctions régulières. Nous allons considérer une structure un peu plus fine, en utilisant une autre algèbre qui n’est pas une algèbre de fonctions. En effet, il est avantageux de pouvoir distinguer, par exemple, l’ensemble algébriqueO 說 k défini par l’équation x = 0 («point simple») du même ensemble défini par l’équation x ² = 0 («point double»), bien que ces ensembles soient isomorphes. Pour cela, on est conduit à associer à l’ensemble algébrique X 說 k ⁿ , défini par les équations f ¹ = 0, f ² = 0, ..., f ^s = 0, non pas l’algèbre de fonctions k [¹, ², ..., Tⁿ ]/I(X), mais l’algèbre k [¹, ², ..., Tⁿ ]/ face=F9828 a, où face=F9828 a est l’idéal de polynômes engendré par f ¹, f ², ..., f ^s ; il est clair que face=F9828 a est contenu dans I(X), donc l’algèbre des fonctions régulières sur X s’identifie à un quotient de la nouvelle algèbre; ainsi, tout élément de cette nouvelle algèbre définit une fonction régulière f sur X (sa classe modulo I|(X)/ face=F9828 a), mais f peut être nulle sans que l’élément considéré le soit. Dans l’exemple deO 說 k , l’algèbre associée est k [T]/(T) 力 k dans le cas du point simple, d’équation x = 0, et k [T]/(T²) 力 k + k 﨎, algèbre des nombres duaux (extension quadratique de k engendrée par un élément 﨎 de carré nul) dans le cas du point double, d’équation x ² = 0; l’élément 﨎 définit une fonction nulle.

Nous appellerons variété algébrique affine un triplet (X, A, 﨏 ) où X est un ensemble, A une k -algèbre engendrée par un nombre fini d’éléments et 﨏 une bijection de X sur Hom^k (A, k ). Notons que si (x ¹, x ², ..., x ⁿ ) est un système de générateurs de A, il détermine un homomorphisme surjectif k [¹, ² ..., Tⁿ ]A dont le noyau face=F9828 a est engendré par un nombre fini de polynômes, car l’anneau des polynômes est noethérien (théorème de Hilbert, cf. ANNEAUX COMMUTATIFS); ainsi A est isomorphe à l’algèbre associée à un ensemble algébrique affine contenue dans k ⁿ , et 﨏 détermine une bijection de X sur cet ensemble. Un morphisme (X, A, 﨏 )(Y, B, 祥) de variétés algébriques affines est un couple (u , v ) d’une application u : XY et d’un homomorphisme v : BA de k -algèbres, tel que 﨏(x ) 獵 v = 祥(u (x )) pour tout point x de X; en fait la connaissance de v détermine entièrement u (à l’aide de 﨏 et 祥). Le composé d’un tel morphisme avec un morphisme (u , v ) : (Y, B, 祥)(Z, C, 﨑) est le morphisme (u 獵 u , v 獵 v ) de (X, A, 﨏) dans (Z, C, 﨑). Le morphisme (u , v ) est un isomorphisme s’il existe un morphisme (u , v ) de (Y, B, 祥) dans (X, A, 﨏) tel que les composés (u , v ) 獵 (u , v ) et (u , v ) 獵 (u , v ) soient les morphismes identiques (id^X, id^A) et (id^Y, id^B); cela revient à dire que v est un isomorphisme de k -algèbres.

La droite affine est la variété (k , k [T], 祥) où 祥 applique tout élément a de k sur l’homomorphisme k [T]k qui transforme T en a. Un morphisme de (X, A, 﨏) dans la droite affine est donc formé d’une application u de X dans k et d’un homomorphisme v de k [T] dans A; la donnée de v , qui équivaut à celle du morphisme (u , v ), revient à celle de l’élément f = v (T) de A; pour tout point x de X on a u (x ) = 﨏 (x )(f ). Autrement dit, les éléments de A correspondent bijectivement aux morphismes de (X, A, 﨏) dans la droite affine (et non plus aux fonctions régulières; un morphisme est une donnée plus riche que la fonction u sous-jacente).

Nos définitions montrent que l’étude des variétés algébriques affines est équivalente à celle des k -algèbres de type fini (c’est-à-dire engendrées par un nombre fini d’éléments). Les principaux résultats de cette théorie sont dus aux géomètres allemands de la première moitié du XX^e siècle. Nous les citerons sans donner de démonstration complète.

Précisons d’abord que si B est un anneau, une B-algèbre A est dite de type fini si elle est engendrée en tant qu’algèbre par un nombre fini d’éléments, tout élément de A s’exprimant comme fonction polynôme de ces générateurs. L’algèbre A est dite finie si elle est engendrée par un nombre fini d’éléments en tant que B-module: tout élément de A est combinaison linéaire des générateurs; cela revient à dire que A est de type fini et entière sur B.

Lemme de normalisation d’Emmi Noether

Soit A une k -algèbre de type fini non nulle, engendrée par n éléments. Il existe un entier d et un homomorphisme injectif v : k [¹, ², ..., T^d ]A, faisant de A une k [¹, ², ..., T^d ]-algèbre finie .

Géométriquement, v s’interprète comme un morphisme de la variété affine X qui correspond à A dans l’espace affine k ^d ; les propriétés de v impliquent que ce morphisme est surjectif et «fini», c’est-à-dire qu’il fait de X une sorte de revêtement ramifié de k ^d .

On peut démontrer ce lemme par récurrence sur le nombre n de générateurs de A 力 k [¹, ², ..., Tⁿ ]/ face=F9828 a; il est évident si face=F9828 a =0, en particulier si n = 0. Dans le cas contraire, on montre qu’il est possible de trouver un nouveau système de n générateurs dont le dernier est entier sur la sous-algèbre A engendrée par les n – 1 premiers, de sorte que A est une A -algèbre finie; on applique alors l’hypothèse de récurrence à 藺 .

Par exemple, si A = k [x , y ]/(f ) est l’algèbre de la courbe plane définie par l’équation f (x , y ) = 0, on fait un changement de base dans k ² de manière que l’axe des y ne soit pas une «direction asymptotique» de la courbe (c’est possible, car k est infini); l’équation de la courbe prend alors la forme :

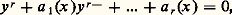où les a ⁱ (x ) sont des polynômes en x. Ainsi la classe de y dans A est entière sur k [x ], et la courbe apparaît comme un revêtement ramifié (de degré r ) de l’axe des x.

Appliquons ce résultat en remplaçant A par le quotient A/ face=F9828 m où face=F9828 m est un idéal maximal de A; ce quotient est encore de type fini sur k , et c’est un corps. D’après le lemme, il contient une sous-algèbre B isomorphe à une algèbre de polynômes, sur laquelle il est une algèbre finie; on en déduit aisément que B est elle-même un corps, et ensuite que B 力 k. Comme k est algébriquement clos, son extension finie A/ face=F9828 m lui est isomorphe. Cela prouve que tout idéal maximal de A est le noyau d’un homomorphisme de A dans k , et permet d’établir une correspondance bijective entre les idéaux maximaux de A et les points de la variété algébrique affine associée à A. Pour développer la géométrie algébrique sur un corps non algébriquement clos, il est raisonnable de remplacer l’ensemble Hom^k (A, k ) par l’ensemble des idéaux maximaux de A dans la définition des variétés algébriques affines; cela revient à considérer, outre les «points rationnels sur k » de la variété, qui correspondent à des idéaux maximaux face=F9828 m tels que A/ face=F9828 m 力 k , d’autres points correspondant à des idéaux maximaux face=F9828 m tels que A/ face=F9828 m soit une extension finie de k. Nous conservons un corps de base algébriquement clos pour rester plus près des notions intuitives.

Considérons une variété algébrique affine (X, A, 﨏); si f 捻 A et x 捻 X, nous noterons f (x ) la valeur en x de la fonction sur X définie par f , c’est-à-dire 﨏 (x ) (f ). Pour qu’un élément de f de A soit inversible, il faut et il suffit que f (x ) 0 pour tout point x de X; en effet, cette condition signifie que f n’appartient à aucun idéal maximal de A, et, d’après le théorème de Krull, un élément non inversible appartient toujours à un idéal maximal ^{[cf. ANNEAUX ET ALGÈBRES]}.

Théorème des zéros de Hilbert

Soit (X, A, 﨏) une variété algébrique affine. Si f 捻 A les conditions suivantes sont équivalentes :

(1) Pour tout point x de X, f (x ) = 0.

(2) L’élément 1 漣 f T est inversible dans l’algèbre de polynômes A[T].

(3) f est nilpotent, c’est-à-dire que l’une de ses puissances est nulle.

La condition (2) sert d’intermédiaire entre (1) et (3); elle s’interprète en disant que 1 漣 f T ne s’annule pas sur la variété affine d’algèbre A[T] (qui n’est autre que X 憐 k , cf. infra ). Ainsi, on voit aisément que (1) implique (2). Pour voir que (2) implique (3), on note que 1 漣 f T admet pour inverse 1 + f T + f ²² + ... f ⁿ Tⁿ + ... dans l’algèbre de séries formelles A [[T]], si cet inverse est un polynôme, f est nilpotent. Enfin, si f est supposé nilpotent, il en est de même de f (x ) pour tout point x ; or f (x ) 捻 k , et dans un corps tout élément nilpotent est nul.

Autrement dit, l’ensemble face=F9828 n des éléments nilpotents de A est l’intersection des idéaux maximaux (c’est un idéal qu’on appelle le nilradical de A). Pour un anneau quelconque, le même raisonnement prouve que le nilradical est l’intersection des idéaux premiers; ici, on voit, en appliquant le théorème précédent à A/ face=F9828 p où face=F9828 p est un idéal premier de A, que tout idéal premier de A est une intersection d’idéaux maximaux (on dit que A est un anneau de Jacobson).

À tout idéal face=F9828 a de A, nous associerons l’ensemble V(face=F9828 a) 說 X des points x tels que f (x ) = 0 pour tout f 捻 face=F9828 a; il suffit d’écrire cette condition pour un système de générateurs (f ¹, f ², ..., f ^s ) de face=F9828 a, et on peut dire que V(face=F9828 a) est un sous-ensemble algébrique de X. Avec l’algèbre A/ face=F9828 a, il forme une variété algébrique affine à laquelle on peut appliquer le théorème précédent. On trouve ainsi que l’idéal I(V (face=F9828 a)) formé des éléments f de A tels que f (x ) = 0 pour tout x 捻 V(face=F9828 a) est égal à la racine face=F9828 w(face=F9828 a) de face=F9828 a c’est-à-dire à l’ensemble des éléments de A qui ont une puissance dans face=F9828 a; en particulier, V(face=F9828 a) n’est pas vide si face=F9828 a A (c’est l’énoncé du Nullstellensatz de Hilbert).

3. Variétés algébriques

L’utilisation des fonctions régulières ne conduit à rien dans l’étude des ensembles algébriques projectifs, puisque l’anneau des fonctions régulières d’un tel ensemble est toujours réduit à k. On peut remplacer les fonctions régulières par les fonctions rationnelles. La théorie ainsi construite permet l’étude des propriétés conservées par une équivalence birationnelle ; elle a été développée à la fin du siècle dernier, principalement en Italie. Cette méthode interdit la distinction entre des ensembles algébriques birationnellement équivalents, même non isomorphes. Il faut donc chercher dans une autre direction pour obtenir une définition intrinsèque des variétés algébriques.

En localisant la notion de fonction régulière, on arrive à une notion adéquate. Commençons par munir les ensembles algébriques d’une topologie qui permette une telle localisation.

Topologie de Zariski

Si le corps de base est celui des nombres complexes, on peut essayer la topologie induite par celle de Cⁿ ou Pⁿ (C) (c’est la topologie transcendante , définie à partir de la valeur absolue d’un nombre complexe). Il est clair, en effet, que les applications régulières sont continues pour cette topologie; par suite, les isomorphismes la conservent. Mais cela ne convient pas au cas d’un corps de base général.

On veut une topologie adaptée à l’étude des propriétés algébriques; ainsi les propriétés algébriques (ou du moins beaucoup d’entre elles) doivent avoir une nature locale pour la topologie cherchée: par exemple, une fonction rationnelle définie en un point doit rester définie au voisinage de ce point. Or les ensembles exceptionnels où les propriétés algébriques considérées cessent d’être vraies sont définis par des équations polynomiales (l’annulation du dénominateur dans le cas de la définition d’une fonction rationnelle); ce sont eux-mêmes des ensembles algébriques. Ainsi, nous imposons la condition suivante: les ensembles algébriques doivent être fermés pour la topologie cherchée. Il se trouve qu’il existe sur k ⁿ , ou sur Pⁿ (k ), une topologie bien déterminée pour laquelle les ensembles fermés sont les ensembles algébriques: on l’appelle la topologie de Zariski.

En effet, l’intersection d’une famille (Eⁱ )ⁱ size=1^捻I d’ensembles algébriques est encore algébrique; si Eⁱ est défini par les équations f ⁱ size=1^凞 = 0, 捻 炙ⁱ , cette intersection est définie par l’annulation de tous les polynômes f ⁱ size=1^凞: c’est l’ensemble des zéros communs aux polynômes de l’idéal engendré par les f ⁱ size=1^凞 et il suffit de prendre un ensemble fini de générateurs de cet idéal pour avoir un système d’équations de l’intersection (rappelons la propriété noethérienne de l’anneau des polynômes; dans le cas projectif, il faut bien sûr prendre des générateurs homogènes). Considérons maintenant la réunion de deux ensembles algébriques, définis respectivement par les équations f ¹ = 0, f ² = 0, ..., f ^r = 0 et g ¹ = 0, g ² = 0, ..., g ^s = 0; c’est l’ensemble des zéros communs aux polynômes f ⁱ g ^j (1 諒 i 諒 r , 1 諒 j 諒 s ), donc un ensemble algébrique. Enfin l’ensemble vide est algébrique, étant défini par l’équation 1 = 0. Ainsi les axiomes des fermés d’une topologie sont vérifiés par les ensembles algébriques (cf. TOPOLOGIE - Topologie générale). Dorénavant nous considérons k ⁿ et Pⁿ (k ) comme munis de leurs topologies de Zariski, et tout ensemble algébrique affine ou projectif est muni de la topologie induite; toute variété algébrique affine est de même munie de sa topologie de Zariski.

Si (X, A, 﨏) est une variété algébrique affine, une base d’ouverts de sa topologie de Zariski est formée des ensembles D(f ) =x 捻 X | f (x ) 0, où f 捻 A. On obtient de même une base d’ouverts sur un ensemble algébrique projectif en considérant les ensembles où ne s’annule pas un polynôme homogène.

Il est clair que les applications régulières sont continues pour la topologie de Zariski: l’image réciproque d’un ensemble algébrique par une telle application est encore algébrique. Ainsi, deux ensembles algébriques isomorphes sont homéomorphes. La réciproque n’est pas vraie, puisque la représentation paramétrique t 料 (t ², t ³) de la cissoïde est un homéomorphisme de k sur cette courbe, qui n’est pourtant pas isomorphe à une droite (cf. chap. 1, Applications régulières ); autrement dit, la topologie de Zariski est insuffisante pour caractériser les ensembles algébriques à isomorphisme près.

Anneaux locaux

À tout point x d’un ensemble algébrique X on peut associer l’anneau 六^X,x , des germes de fonctions rationnelles sur X définies en x ; un tel germe est une classe d’équivalence de fonctions rationnelles définies en x , pour la relation qui consiste à confondre deux fonctions lorsqu’elles coïncident dans un voisinage de x. Ainsi un élément de 六^X,x est représenté par une fraction P/Q dont le dénominateur Q ne s’annule pas en x ; dans le cas projectif, les polynômes P et Q sont homogènes de même degré. Pour qu’un tel élément soit inversible, il faut et il suffit que son numérateur P ne s’annule pas en x ; autrement dit, l’ensemble des éléments non inversibles de 六^X,x est l’idéal face=F9828 m^x , noyau de l’homomorphisme f 料 f (x ) à valeurs dans k , et c’est le seul idéal maximal de l’anneau. Un anneau qui possède un seul idéal maximal est dit local ; nous avons muni l’ensemble algébrique X d’un anneau local 六^X,x pour chaque point x.

Si une application rationnelle u : XY est définie en un point x de l’ensemble algébrique X, il lui correspond un homomorphisme g 料 g 獵 u de l’anneau local 六^Y,u(x) dans 六^X,x ; cet homomorphisme applique l’idéal maximal du premier anneau dans celui du second, ce qu’on exprime en disant que c’est un homomorphisme local. Si (u , v ) est une équivalence birationnelle entre X et Y, elle définit une bijection entre des ouverts de Zariski partout denses U et V de X et Y de manière que les anneaux locaux en des points correspondants de U et V soient isomorphes; cela s’applique en particulier à un isomorphisme de X sur Y, avec U = X et V = Y.

On peut donner trois exemples :

– Les fonctions rationnelles sur la droite k forment le corps k (x ) (corps des fractions de l’anneau des polynômes k [x ]). Comme les voisinages ouverts au sens de Zariski d’un point a sont des complémentaires d’ensembles finis, deux fonctions rationnelles qui coïncident au voisinage de a sont identiques, et l’anneau local de a n’est autre que l’ensemble des fractions dont le dénominateur n’est pas nul en a.

– Il est facile de voir que les fonctions rationnelles sur la courbe d’équation y ² = x ³ s’écrivent d’une manière unique sous la forme R(x ) + y S(x ), où R et S sont des éléments de k (x ); ainsi l’ensemble des fonctions rationnelles sur la cissoïde est un corps, extension quadratique de k (x ) engendrée par un élément y qui vérifie y ² = x ³. L’anneau local d’un point (a , b ) s’identifie à l’ensemble des éléments R(x ) + y S(x ) tels que R et S soient définies en a. Comme les applications u : t 料 (t ², t ³) (application régulière) et v = y /x (application rationnelle définie sauf en (0, 0)) forment une équivalence birationnelle entre la droite et la cissoïde X, les anneaux locaux sur X aux points (a , b ) (0, 0) sont isomorphes à ceux des points correspondants sur la droite. Au contraire, l’anneau local, 六^X,(0,0) n’est pas intégralement clos (il ne contient pas l’élément entier y /x ), tandis que tous les anneaux locaux sur la droite sont intégralement clos. On voit donc que le point de rebroussement de la cissoïde se manifeste dans les propriétés des anneaux locaux (fig. 2).

– Un raisonnement analogue permet d’étudier le cône d’équation z ² = x ² + y ² dans k³. Les fonctions rationnelles sur cette surface forment un corps, extension quadratique de k (x , y ); elles s’écrivent R(x , y ) + z S(x , y ). L’anneau local de l’origine est formé de ceux de ces éléments pour lesquels les fractions R et S sont définies en (0, 0), et son idéal maximal est défini par la condition R(0,0) = 0.

Faisceau structural

La connaissance de la topologie et des anneaux locaux sur un ensemble algébrique est insuffisante pour caractériser cet ensemble à isomorphisme près; en particulier, elle ne permet pas de reconstituer l’algèbre des fonctions régulières sur l’ensemble. Nous allons remplacer les anneaux locaux par une structure plus riche.

Considérons un ouvert de Zariski U dans un ensemble algébrique X. Nous dirons qu’une application de U dans k est une fonction régulière dans U si son germe en chaque point x de U appartient à l’anneau local 六^X,x ; l’ensemble des fonctions régulières dans U forme un anneau (et même une k -algèbre), que nous noterons 六^X(U). Notre terminologie n’est pas contradictoire, car 六^X(X) est précisément l’ensemble des fonctions régulières sur X, en vertu du théorème :

Soient X un ensemble algébrique et f : Xk une application de X dans k. On suppose que pour tout point x de X il existe un voisinage V^x de x et une fonction rationnelle r ^x définie dans V^x et telle que f |^Vx = r ^x. Alors f est une fonction régulière.

Ce résultat se démontre ainsi, dans le cas où X est affine: on peut supposer que les voisinages V^x sont de la forme D(g ^x) (ensemble des points où g ^x ne s’annule pas), avec des fonctions régulières g ^x. Comme les D(g ^x) recouvrent X, l’idéal engendré par les fonctions g ^x est l’anneau A de toutes les fonctions régulières sur X (sinon on pourrait trouver un idéal maximal contenant les g ^x, donc un point de X où toutes ces fonctions s’annulent); par suite, 1 est combinaison linéaire d’un nombre fini de fonctions g ^x soient g ¹, g ², ..., g ^s et X = D(g ¹) 聆 D(g ²) 聆 ... 聆 D(g ^s ). Dans l’ouvert D(g ⁱ ), f coïncide avec une fonction rationnelle r ⁱ définie dans D(g ⁱ ); ici nous avons besoin d’un lemme: toute fonction rationnelle définie dans D(g ⁱ ) peut s’écrire sous la forme h /g ^{i m} où h est une fonction régulière et m un entier (car g ⁱ s’annule sur l’ensemble des zéros du dénominateur, donc, par le Nullstellensatz , ce dénominateur divise une puissance de g ⁱ ). Nous pouvons donc trouver un entier m et des fonctions régulières h ¹, h ², ..., h ^s tels que g ^{i m} f coïncide avec h ⁱ dans D(g ⁱ ); dans D(g ⁱ ) 惡 D(g ⁱ ) = D(g ⁱ g ^j ), les fonctions g ^{i m} h ^j et g ^{j m} h ⁱ sont égales, et par suite leur différence est annulée par g ⁱ g ^j . Il existe des fonctions régulières f ¹, f ², ..., f ^s telles que f ¹g ^1m+1 + f ²g ^2m+1 + ... + f ^s g ^{s m+1} = 1, car les D(g ^{i m+1} ) recouvrent X; on peut alors vérifier que f coïncide avec f ¹g ¹h ¹ + f ² g ² h ² + ... + f ^s g ^s h ^s dans chaque D(g ⁱ ), donc lui est égale.

On appelle faisceau d’anneaux sur un espace topologique X un couple (A, 福) du type suivant: A associe à chaque ouvert U de X un anneau A(U) et 福 associe à chaque couple (U, V) d’ouverts tels que U 說 V un homorphisme 福^UV: A(V)A(U) appelé restriction de V à U. On impose à ces données les conditions suivantes:

(1) Pour tout ouvert U, l’homomorphisme 福^UU est l’application identique de A(U). Si U 說 V 說 W, on a 福^UW = 福^UV 獵 福^VW.

(2) Pour tout ouvert U et tout recouvrement (Uⁱ )ⁱ size=1^捻I de U par des ouverts, l’application f 料 ( 福^{Ui U}(f )) est une bijection de A(U) sur l’ensemble des familles :

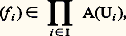telle que les restrictions de f ⁱ et f ^j à Uⁱ 惡 U^j soient égales pour tout couple (i , j ) d’indices. Cela signifie qu’un élément de A(U) est connu quand on connaît ses restrictions à tous les Uⁱ , et donne la condition pour que des éléments des A(Uⁱ ) proviennent par restriction d’un même élément de A(U).

La fibre A^x du faisceau en un point x de X est la limite inductive des A(U) lorsque U parcourt l’ensemble filtrant des voisinages ouverts de x ; pour construire cette limite inductive, on identifie des éléments de A(U) et A(V), où U et V sont des voisinages ouverts de x , si leurs restrictions à un voisinage W 說 U 惡 V sont égales; les classes d’équivalence ainsi définies sont les éléments de A^x .

Il est clair que les anneaux de fonctions 六^X(U) que nous avons définis sur un ensemble algébrique X forment un faisceau d’anneaux (avec la notion habituelle de restriction). Les fibres sont les anneaux locaux 六^X,x . Considérons une application régulière u : XY d’ensembles algébriques; elle est continue pour les topologies de Zariski, de sorte que si V est un ouvert de Y, u ^-1(V) est un ouvert de X. On a alors un homomorphisme g 料 g 獵 u de 六^Y(V) dans 六^X(u ^-1(V)). D’une manière générale, on appelle espace localement annelé un espace topologique X muni d’un faisceau d’anneaux (A, 福) dont les fibres sont des anneaux locaux. Un morphisme d’espaces localement annelés de (X, (A, 福)) dans (Y, (B, 靖)) est un couple (u , v ) où u est une application continue de X dans Y et v associe à chaque ouvert V de Y un homomorphisme v ^v: B(V) 轢A(u ^-1(V)) de manière compatible avec les restrictions 福 et 靖. On impose de plus que, pour tout point x de X, l’homomorphisme v ^x : B^u(x)A^x déduit de v soit un homomorphisme local. Il est facile de définir le morphisme composé de deux morphismes, puis la notion d’isomorphisme entre espaces localement annelés.

Soit U un ouvert d’un espace localement annelé (X, (A, 福)). La topologie induite et le faisceau induit A|^U : U 料 A(U ), pour U ouvert contenu dans U, font de U un espace localement annelé; on dit que c’est un sous-espace ouvert de X. Par exemple, si X est un ensemble algébrique affine et si f est une fonction régulière sur X, l’ensemble D(f ) des points de X où f n’est pas nulle, muni de la structure d’espace annelé induite par celle de X, est un sous-espace ouvert de X. Si X est défini, dans k ⁿ , par les équations g ¹ = 0, g ² = 0, ..., g ^s = 0, et si f est la restriction à X d’un polynôme f 捻 k [x ¹, x ², ..., x ⁿ ], alors D(f ) est la projection sur k ⁿ de l’ensemble algébrique Y 說 k ⁿ⁺¹ = k ⁿ 憐 k défini par les équations g ¹ = 0, g ² = 0, ..., g ^s = 0 et 1 漣 tf = 0. La projection: (x , t ) 料 x définit un isomorphisme d’espaces localement annelés de Y sur D(f ). Par exemple, le complémentaire de 0 dans la droite k est isomorphe, comme espace localement annelé, à l’hyperbole d’équation xt = 1 dans le plan des (x , t ) (fig. 5).

Nous pouvons aussi munir D(f ) d’une structure de variété algébrique affine, en transportant celle de Y. Soit A = k [x ¹, x ², ... x ⁿ ]/ face=F9828 a l’algèbre de la variété affine X, où face=F9828 a est l’idéal engendré par g ¹, g ², ..., g ^s . L’algèbre de Y est k [x ¹, x ², ..., x ⁿ ,t ]/ face=F9828 b où face=F9828 b est engendré par g ¹, g ², ..., g ^s et 1 漣 tf ; elle est isomorphe à A^f = A[t ]/(1 漣 tf ), en désignant par f la classe de f dans A. Dorénavant, si (X, A, 﨏) est une variété algébrique affine et si g est un élément de A, nous munirons l’ouvert D(f ) des points de X où f n’est pas nul d’une structure de variété algébrique affine au moyen de l’algèbre A^f = A[t ]/(1 漣 tf ); les éléments de cette algèbre peuvent s’écrire comme des fractions du type h /f ^r où h 捻 A (notons qu’une telle fraction est nulle dès que h est annulé par une puissance de f , soit f ^m h = 0 ; cela n’exige pas que h soit nul). On peut montrer qu’il existe sur X un faisceau 六^X et un seul qui prennent la valeur A^f dans l’ouvert D(f ) pour tout f 捻 A. Si U est un ouvert de X, les éléments de 六^X(U) ne sont pas des fonctions dans U, mais chacun d’eux définit une fonction (régulière) dans U; cette fonction est nulle si, et seulement si, l’élément considéré est nilpotent. La fibre de 六^X,x en un point x est un anneau local, dont les éléments s’écrivent comme des fractions h /g avec h , g 捻 A et g (x ) 0; ainsi (X, face=F0021 六^X) est un espace localement annelé.

Si (u , v ): (X, A, 﨏)(Y, B, 祥) est un morphisme de variétés algébriques affines, on en déduit aisément un morphisme (u , v ): (X, face=F0021 六^X)(Y, face=F0021 六^Y) en définissant v ^D(g) , pour g 捻 B, comme l’homomorphisme de B^g dans A^v(g) qui transforme h /g ^r en v (h )/(g )^r . Inversement, si (u , w ): (X, face=F0021 六^X)(Y, face=F0021 六^Y) est un morphisme d’espaces localement annelés, (u , w ^Y) est un morphisme de variétés affines; on a (v )^Y = v et (w ^Y) = w. Cela implique en particulier que deux variétés algébriques affines sont isomorphes si, et seulement si, elles sont isomorphes comme espaces localement annelés. Dans la suite, nous considérerons les variétés algébriques affines comme des espaces localement annelés.

Considérons maintenant un ensemble algébrique X défini dans l’espace projectif Pⁿ (k ) par des équations homogènes g ¹ = 0, g ² = 0, ..., g ^s = 0, et un polynôme f homogène de degré d par rapport aux coordonnées homogènes x ⁰, x ¹, ..., x ⁿ . Soit D⁺(f ) l’ensemble ouvert des points de X où f n’est pas nul, muni de la structure annelée induite par celle de X; il est isomorphe à un ensemble algébrique affine. On le voit tout de suite si f = x ⁰, en utilisant l’isomorphisme connu de k ⁿ sur le complémentaire de l’hyperplan d’équation x ⁰ = 0 dans Pⁿ (k ); si d = 1, un changement de coordonnées nous ramène à ce cas facile. Le cas général se ramène au cas où d = 1 en identifiant Pⁿ (k ) à la variété de Veronese V^{n ,d} (cf. chap. 1).

Cela permet encore de munir D⁺(f ) d’une structure de variété algébrique affine, dont l’algèbre est obtenue ainsi: soit face=F9828 a l’idéal homogène de polynômes engendré par g ¹, g ², ..., g ^s , et soit A = k [x ⁰, x ¹, ..., x ⁿ ]/ face=F9828 a l’algèbre graduée quotient; désignons par A^(d) la sous-algèbre de A formée des éléments dont le degré est un multiple de d ; l’algèbre de D⁺(f ) est A^(f) = A^(d) /(f 漣 1) et ses éléments s’écrivent comme des fractions h /f ^r où h est un élément de degré rd de A. Il existe alors un faisceau d’anneaux bien déterminé sur X qui prend la valeur A^(f) sur D⁺(f ); sa fibre en un point x est un anneau local, dont les éléments sont les fractions du type h /g avec h , g 捻 A homogènes de même degré et g non nul en x. Nous désignerons ce faisceau par 六^X, et nous dirons que l’espace localement annelé (X, face=F0021 六^X) est une variété algébrique projective. On peut montrer que pour tout morphisme d’espaces localement annelés (u , w ): (X, face=F0021 六^X)(Y, face=F0021 六^Y) entre des variétés algébriques projectives, l’application u est régulière (on commence par observer que la restriction de u à tout ouvert affine de la forme D⁺(f ) 說 X est régulière).

La notion d’espace localement annelé nous a permis de traiter de manière analogue les variétés algébriques affines ou projectives. De plus, toute variété algébrique projective X 說 Pⁿ (k ) peut être recouverte par des ouverts Uⁱ qui sont des variétés affines pour la structure induite; on peut même prendre des Uⁱ en nombre fini, par exemple Uⁱ = D⁺(x ⁱ ) (x ⁱ coordonnées homogènes). D’une manière générale, nous dirons qu’un espace localement annelé (X, face=F0021 六^X) est une variété algébrique s’il existe un recouvrement (Uⁱ ) de X par des ouverts qui sont isomorphes (pour la structure localement annelée induite) à des variétés algébriques affines.

4. Propriétés élémentaires

Tout ouvert U d’une variété algébrique X, muni de la structure annelée induite, est une variété algébrique; on dit que c’est une sous-variété ouverte de X.

Considérons un faisceau d’idéaux 琉 de 六^X (c’est-à-dire un faisceau tel que 琉(U) soit un idéal de 六^X(U) pour tout ouvert U, les opérations de restriction de 琉 étant induites par celles de 六^X); on peut définir un faisceau quotient 六^X/ 琉, dont la fibre en un point x quelconque de X est 六^X,x / 琉^x . Si 琉 est «localement de type fini», le support Y de ce faisceau quotient, c’est-à-dire l’ensemble des points x où sa fibre n’est pas nulle, est une partie fermée de X. On peut considérer 六^X/ 琉 comme un faisceau sur Y, et Y muni de ce faisceau est une variété algébrique; on dit que c’est une sous-variété fermée de X. Par exemple, les variétés algébriques affines (resp. projectives) peuvent être considérées comme des sous-variétés fermées d’un espace k ⁿ (resp. Pⁿ (k )).

Si Y est un fermé quelconque de X, le faisceau d’idéaux 琉^Y formé des f qui s’annulent sur Y est localement de type fini et 六^X/ 琉^Y a pour support Y, d’où sur Y une structure de sous-variété fermée de X. Ce n’est pas la seule possible, mais on peut la caractériser par le fait qu’elle est réduite , c’est-à-dire que son faisceau structural ne comporte pas d’éléments nilpotents non nuls (il s’interprète comme un faisceau de fonctions sur Y). En particulier, si Y = X, on définit une sous-variété fermée X^red de X qui est réduite et a même espace topologique sous-jacent que X.

Sur l’ensemble produit X 憐 Y de deux variétés algébriques, on peut définir une structure de variété algébrique munie de morphismes p : X 憐 YX et q : X 憐 YY, de manière que les morphismes u d’une variété Z dans X 憐 Y correspondent bijectivement aux couples (p 獵 u , q 獵 u ) de morphismes de Z dans X et Y respectivement. En général la topologie de X 憐 Y est strictement plus fine que la topologie produit. Par exemple k ^m 憐 k ⁿ 力 k ^m+n ; le produit de deux variétés affines est par suite une variété affine. De même, le produit de deux variétés projectives est projective; en effet, P^m (k ) 憐 Pⁿ (k ) s’identifie à une sous-variété fermée de P^r (k ), avec r = mn + m + n , au moyen du morphisme de Segre qui transforme un couple (x , y ) 捻 P^m (k ) 憐 Pⁿ (k ) en le point de coordonnées homogènes x ⁱ y ^j (0 諒 i 諒 m , 0 諒 j 諒 n ) où les x ⁱ sont les coordonnées homogènes de x et les y ^j celles de y . Par exemple, pour m = n = 1, le morphisme de Segre P¹(k ) 憐 P¹(k )P³(k ) identifie le produit de deux droites projectives à la quadrique d’équation homogène zt = xy (cf. chap. 1, exemple des paraboloïdes et fig. 3); lorsque a décrit P¹(k ), l’image dea 憐 P¹(k ) décrit l’un des systèmes de génératrices rectilignes de la quadrique, tandis que l’image de P¹(k ) 憐a décrit l’autre système.

On dit qu’une variété algébrique X est séparée si la diagonale ^X =(x , x ) | x 捻 臨X est une partie fermée de X 憐 X (comme la topologie de X 憐 X est plus fine que la topologie produit, cela ne signifie pas en général que la topologie de X est séparée). Une sous-variété (ouverte ou fermée) d’une variété séparée est aussi séparée; de même, un produit de variétés séparées est séparé. L’espace k ⁿ et l’espace Pⁿ (k ) sont séparés, donc les variétés algébriques affines ou projectives sont séparées.

La propriété noethérienne des algèbres de type fini se traduit dans le fait que toute suite décroissante de fermés d’une variété algébrique affine est stationnaire. Il en résulte que tout sous-espace d’une telle variété est quasi compact, c’est-à-dire vérifie l’axiome de Borel-Lebesgue ^{[cf. TOPOLOGIE]}. Les variétés algébriques qui sont quasi compactes sont celles qui admettent un recouvrement fini par des ouverts affines; il en est ainsi pour les variétés affines ou projectives. Les variétés algébriques au sens de Serre sont supposées réduites, séparées et quasi compactes.

Une variété non vide qui n’est pas réunion de deux fermés strictement plus petits est dite irréductible ; il revient au même de dire que tout ouvert non vide est partout dense. L’espace k ⁿ et l’espace Pⁿ (k ) sont irréductibles. Toute variété algébrique quasi compacte est réunion d’un nombre fini de composantes irréductibles , qui sont ses parties fermées irréductibles maximales.

La dimension d’une variété algébrique X est définie comme la borne supérieure de l’ensemble des entiers n pour lesquels il existe une suite strictement croissante de (F⁰, ¹, ..., Fⁿ ) de fermés irréductibles de X; c’est un nombre fini si X est quasi compacte. Si X est une variété intègre, c’est-à-dire irréductible et réduite, on peut définir des fonctions rationnelles sur X; ces fonctions forment un corps K(X), extension de type fini de k dont le degré de transcendance est égal à la dimension de X ^{[cf. CORPS]}. Ainsi l’espace k ⁿ et l’espace Pⁿ (k ) sont de dimension n , leur corps de fonctions rationnelles étant k (x ¹, x ², ..., x ⁿ ).

Si k est le corps des nombres complexes, on peut considérer k ⁿ = Cⁿ , comme une variété analytique complexe. Toute variété algébrique affine X, sous-variété fermée de Cⁿ peut alors être munie d’une structure d’espace analytique X^an sous-espace analytique fermé de Cⁿ (la topologie de X^an est induite par la topologie transcendante de Cⁿ et son faisceau structural est quotient du faisceau des fonctions analytiques; cf. FONCTIONS ANALYTIQUES – Fonctions analytiques de plusieurs variables complexes). Considérons maintenant une variété algébrique X sur C, recouverte par des ouverts affines Uⁱ ; les structures analytiques U^{i an} se recollent et définissent sur X une structure d’espace analytique X^an , de même dimension que X. Un grand nombre de propriétés de géométrie algébrique concernant X se traduisent par des propriétés analytiques de X^an .

Par exemple, on peut définir la notion de point régulier d’une variété algébrique X; si le corps de base est C, pour qu’un point x de X soit régulier, il faut et il suffit que X^an soit une variété analytique sans singularité au voisinage de x. Ainsi, tout point de Cⁿ ou de Pⁿ (C) est régulier, mais O n’est pas un point régulier de la cissoïde représentée dans la figure 2 (on dit que c’est un point singulier). L’ensemble des points réguliers d’une variété algébrique est ouvert, et il est partout dense si la variété est réduite. L’anneau local en un point régulier est factoriel ^{[cf. ANNEAUX COMMUTATIFS]}.

Comme autre exemple, considérons la notion de variété algébrique complète (définie sur un corps de base arbitraire). Dans le cas où le corps de base est C, pour que X soit complète il faut et il suffit que X^an soit compact. On voit ainsi que Pⁿ (C) et que les variétés algébriques projectives sont des variétés complètes. Au contaire, les variétés affines de dimension non nulle ne sont pas complètes.

Dans la suite de cet article, nous remplaçons les définitions de certaines notions de géométrie algébrique par leurs traductions transcendantes, en nous restreignant au cas où le corps de base est C; c’est le point de vue de la géométrie italienne du siècle dernier (on démontrait alors les théorèmes par des méthodes transcendantes). Nous pourrons ainsi énoncer un certain nombre de résultats sans être entraînés à des développements trop longs; cependant, ces résultats conservent leur sens et leur validité avec un corps de base général.

5. Morphismes finis. Normalisation et désingularisation

On dit qu’un morphisme f = (u , v ) : XY de variétés algébriques affines est fini si v ^Y : BA fait de A une B-algèbre finie (A désigne l’algèbre de X et B celle de Y). Plus généralement, un morphisme f : XY entre des variétés algébriques quelconques est dit fini s’il existe un recouvrement de Y par des ouverts affines Uⁱ tels que les ouverts f ^-1(Uⁱ ) de X soient affines et que les restrictions :

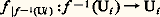soient finies. Un morphisme fini transforme les fermés de X en fermés de Y, et, pour tout point y de Y, la fibre f ^-1(y ) est finie et discrète. Le lemme de normalisation de Noether, énoncé au chapitre 2, signifie que si X est une variété algébrique affine, il existe un morphisme fini et surjectif de X sur un espace k ^d ; l’entier d est égal à la dimension de X. Si X est une sous-variété fermée d’une variété Y, le morphisme d’injection XY est fini.

Soit f : XY un morphisme de variétés algébriques tel que pour tout point y de Y la fibre f ^-1(y ) soit finie et discrète. En général f n’est pas fini, mais, si on le suppose séparé (cela signifie que ^X =(x , x ) | x 捻 X est fermé dans le «produit fibré» X 憐 ^YX; c’est toujours vrai si X est séparé), on peut montrer qu’il existe une variété algébrique X dans laquelle X se plonge comme sous-variété ouverte de manière que f se prolonge en un morphisme fini de X dans Y. Ce résultat, profond et difficile, est connu sous le nom de théorème principal de Zariski.

Un point x d’une variété algébrique X est dit normal si l’anneau local 六^X,x est intègre et intégralement clos. Sur le corps des complexes, cela revient à dire que x est un point normal de X^an , c’est-à-dire que toute fonction analytique définie seulement aux points réguliers voisins de x et bornée se prolonge en une fonction analytique définie dans un voisinage de x. Un point régulier est normal; sur une courbe la réciproque est vraie, mais pas en dimension plus grande. Par exemple, le sommet O du cône d’équation z ² = x ² + y ² dans k ³ est normal sans être régulier (cf. chap. 3 et fig. 6). En un point normal x , chaque composante irréductible de l’ensemble S des points singuliers est de codimension au moins 2; par exemple, si X est une courbe, x a un voisinage qui ne contient aucun point singulier; si X est une surface, il existe un voisinage de x qui ne contient pas d’autre singularité que x.

Soit X une variété algébrique affine intègre, d’algèbre A. On démontre que la clôture intégrale A 黎 de A (ensemble des éléments du corps K(X) qui sont entiers sur A; cf. ANNEAUX COMMUTATIFS) est finie sur A; il lui correspond une variété algébrique affine X 黎 dont tous les points sont normaux, munie d’un morphisme fini X 黎X. On généralise ce résultat en associant à toute variété réduite X une variété normale X 黎 et un morphisme 神 : X 黎X fini et surjectif qui induit un isomorphisme de X 漣 神^-1(Z) sur X 漣 Z en désignant par Z l’ensemble des points de X qui ne sont pas normaux (c’est un fermé sans point intérieur); les variétés X 黎 et X sont birationnellement équivalentes. Lorsque X est une courbe, X 黎 est une courbe sans point singulier; par exemple si X est unicursale et affine, X 黎 est isomorphe à k , et 神 donne une représentation paramétrique de X (cf. fig. 2 et fig. 7).

Il est beaucoup plus difficile d’éliminer d’une manière analogue les singularités des variétés de dimension plus grande. Ce problème a été résolu par S. Abhyankar pour les surfaces et par H. Hironaka pour les variétés de dimension quelconque sur un corps de caractéristique 0; on associe à une variété algébrique X une variété X sans point singulier et un morphisme surjectif 﨏 : X X (non fini en général) qui est une équivalence birationnelle et un isomorphisme de X 漣 﨏^-1(S) sur X 漣 S (S désignant l’ensemble des points singuliers de X).

6. Faisceaux cohérents et cohomologie

Les méthodes cohomologiques sont, comme dans la théorie des espaces analytiques, un des outils les plus puissants de la géométrie algébrique (cf. FONCTIONS ANALYTIQUES – Fonctions analytiques de plusieurs variables complexes et TOPOLOGIE - Topologie algébrique). La topologie de Zariski permet de développer une théorie de la cohomologie à valeur dans les faisceaux algébriques cohérents sur les variétés algébriques.

Considérons une variété algébrique (X, face=F0021 六^X). On définit un faisceau de 六^X-modules 杻, ou faisceau algébrique sur X, en associant à chaque ouvert U de X un 六^X(U)-module 杻(U) et en se donnant, pour U 說 V, des opérations de restriction 杻(V)杻(U) «semi-linéaires» relativement à celles de 六^X. Ces données sont soumises à des axiomes (1) et (2) analogues à ceux énoncés au chapitre 3 pour les faisceaux d’anneaux. La fibre :

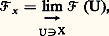en un point x de X est un 六^X,x -module. Un morphisme u d’un faisceau algébrique 杻 dans un autre est la donnée, pour chaque ouvert U de X, d’une application 六^X(U)-linéaire de u ^U de 杻(U) dans (U); si U 說 V, on impose que u ^U et u ^V soient compatibles avec les restrictions de V à U dans 杻 et . Par exemple, si X est une variété algébrique affine, d’algèbre A, et si M est un A-module, on peut lui associer un faisceau algébrique M 黎 dont la valeur dans un ouvert D(f ) de X avec f 捻 A, est M^f = M[t ]/(1 漣 tf )M[t ] (les éléments de M^f se représentent comme des fractions m /f ^r avec m 捻 M); à toute application A-linéaire v : Mぅ entre A-modules correspond un morphisme v : M 黎N 黎 de faisceaux algébriques; le faisceau 六^X est égal à A 黎.

On peut montrer que le fait, pour un faisceau algébrique 杻 sur la variété affine X, d’être isomorphe à un faisceau M 黎, où M est un A-module, est une propriété locale. On peut donc définir une propriété correspondante sur toute variété algébrique. Nous dirons qu’un faisceau algébrique 杻 sur une variété algébrique X est cohérent s’il existe un recouvrement de X par des ouverts affines Uⁱ d’algèbres Aⁱ et des Aⁱ -modules de type fini Mⁱ tels que la restriction de 杻 à Uⁱ soit isomorphe à M 黎ⁱ pour tout i. Par exemple, si 神 : EX est un fibré vectoriel algébrique localement trivial (cf. TOPOLOGIE - Topologie algébrique), on lui associe un faisceau cohérent 劉 dont la valeur dans un ouvert U est l’ensemble des morphismes 靖 : UE tels que 神 獵 靖 soit l’injection canonique de U dans X («sections de E au-dessus de U»); le faisceau 劉 est même localement libre, c’est-à-dire qu’on peut choisir les ouverts Uⁱ de manière que 劉 |Uⁱ 力 M 黎ⁱ où Mⁱ est un module libre de type fini.

À un faisceau algébrique cohérent 杻 sur une variété algébrique X, on associe les groupes de cohomologie Hⁿ (X, face=F0021 杻) (n 捻 N) (cf. TOPOLOGIE - Topologie algébrique); on a H⁰(X, face=F0021 杻) = 杻(X). Si X est affine, Hⁿ (X, face=F0021 杻) = 0 pour n 閭 1 et pour tout faisceau cohérent 杻; cette propriété (analogue au théorème B de Cartan en géométrie analytique, cf. FONCTIONS ANALYTIQUES Fonctions analytiques de plusieurs variables complexes) caractérise les variétés algébriques affines.

Pour étudier la cohomologie d’une sous-variété fermée de l’espace projectif P^r (k ), on utilise le faisceau fondamental 六(1) ainsi défini. Désignons par 神 l’application canonique k ^r+1 漣O sur P^r (k ), et considérons la sous-variété algébrique E de P^r (k ) 憐 k ^r+1 définie par les conditions 﨡 = 0 ou 﨡 0 et 神( 﨡) = x (x 捻 P^r (k ), 﨡 捻k ^r+1 ), et obtenue en faisant «éclater O» dans k ^r+1 (cf. fig. 3 pour le cas r = 1); c’est un sous-fibré vectoriel de rang 1 du fibré trivial P^r (k ) 憐 k ^r+1 de base P^r (k ) et de fibre k ^r+1 . Le faisceau 六(1) des sections du fibré dual E est localement libre de rang 1 et H⁰(P^r , 六(1)) s’identifie à l’ensemble des formes linéaires sur k ^r+1 ; sa puissance tensorielle n -ième, notée 六(n ), est encore un faisceau localement libre de rang 1 et H⁰(P^r , 六(n )) s’identifie à l’ensemble des polynômes homogènes de degré n sur k ^r+1 . Si X est une sous-variété fermée de P^r (k ), nous désignerons par 六^X(1) le faisceau des sections du dual de E^X = X 憐 ^Pr E, et par 六^X(n ) la puissance tensorielle n -ième de ce faisceau; ce sont des faisceaux localement libres de rang 1 sur X; enfin, si 杻 est un faisceau algébrique cohérent sur X, le produit tensoriel :

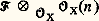est noté 杻(n ). J.-P. Serre a démontré que, pour un faisceau cohérent 杻 donné, il existe un entier n ⁰ tel que H^q (X, face=F0021 杻(n )) = 0 pour n 閭 n ⁰ et q 閭 1. De plus H^q (X, face=F0021 杻) est un k -espace vectoriel de dimension finie pour tout q et s’annule pour q 礪 dim X. Plus généralement H^q (X, face=F0021 杻) est de dimension finie sur k pour tout q lorsqu’on suppose seulement que X est complète.

Lorsque k = C, à tout faisceau algébrique cohérent 杻 sur une variété algébrique X correspond un faisceau analytique cohérent 杻^an sur l’espace analytique X^an . Si X est projective, on a Hⁿ (X, face=F0021 杻) = Hⁿ (X^an , 杻^an ) pour tout n ; on peut en déduire que tout sous-espace analytique fermé Y de P^r (C) est de la forme X^an où X est une variété algébrique (théorème de Chow ) et que tout faisceau analytique cohérent sur Y est de la forme 杻^an où 杻 est un faisceau algébrique cohérent bien déterminé sur X.

Considérons une variété algébrique X sur le corps des nombres complexes. Les propriétés topologiques de X^an (topologie transcendante) se manifestent dans les groupes de cohomologie à valeur dans des faisceaux constants, par exemple dans les groupes Hⁿ (X^an , Z) (cf. TOPOLOGIE - Topologie algébrique). Les groupes correspondants calculés sur X avec la topologie de Zariski n’ont pas les propriétés raisonnables attendues, car la topologie de Zariski est trop grossière; par exemple, il existe des «revêtements» YX (ou Y^an sur un revêtement de X^an ) qui ne sont pas localement triviaux pour la topologie de Zariski. Cependant Grothendieck est parvenu à construire une théorie cohomologique valable sur un corps de base général et donnant de bons groupes de cohomologie à valeur dans des faisceaux constants (cohomologie étale ); si k = C, la cohomologie étale à valeur dans Z/n Z coïncide avec la cohomologie transcendante. À partir des mêmes idées, on peut même développer une théorie de l’homotopie des variétés algébriques (M. Artin).

7. Intersections

Définitions

Soit Y un fermé irréductible d’une variété algébrique X. La codimension de Y dans X est définie comme la borne supérieure des entiers n tels qu’il existe une suite strictement croissante (F⁰, ¹, ..., Fⁿ ) de fermés irréductibles de X avec ⁰ = Y; si X est irréductible :

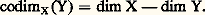Supposons maintenant que X est une variété sans point singulier, et considérons des fermés irréductibles Y et Z de X; si W est une composante irréductible de Y 惡 Z, on a l’inégalité suivante :

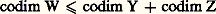(par exemple, dans l’intersection de deux hypersurfaces, toutes les composantes irréductibles sont de codimension au plus 2). On dit que Y et Z se coupent proprement en W dans le cas où il y a égalité :

(formule des dimensions); on peut alors définir un entier m ^w appelé multiplicité de W dans l’intersection de Y et Z (cf. COURBES ALGÉBRIQUES, pour le cas où Y et Z sont des courbes). Si Y et Z se coupent proprement en toutes les composantes irréductibles de Y 惡 Z, on dit que l’intersection de Y et Z est propre, et on peut définir un « cycle » intersection :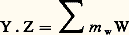

(somme étendue aux composantes irréductibles de Y 惡 Z). D’une manière générale, nous appellerons cycle de codimension m une combinaison linéaire formelle à coefficients entiers de fermés irréductibles de codimension m , et nous désignerons par Z^m (X) le groupe additif des cycles de codimension m. On peut aussi définir la notion de cycles qui se coupent proprement; si z 捻 Z^m (X) et z 捻 Z^m (X) sont des cycles qui se coupent proprement, leur produit d’intersection z.z est défini, et c’est un cycle de codimension m + m . Voici les propriétés fondamentales du produit d’intersection :

(1) Soit z 捻 Z^m (X) et z ¹, z ² 捻 Z^m (X); si z.z ¹ et z.z ² sont définis, il en est de même de z .(z ¹ + z ²) et z .(z ¹ + z ²) = z .z ¹ + z.z ².

(2) Commutativité: z.z = z .z (si l’un des membres est défini, l’autre l’est aussi).

(3) Associativité: z. (z .z ) = (z.z ).z lorsque les deux membres sont définis.

Soit z 捻 Z^m (X) et T 捻 Zⁿ (Y) où X et Y sont des variétés sans singularité; on définit un cycle produit z 憐 t 捻 Z^m+n (X 憐 Y)

Alors si z.z et t.t sont définis, il en est de même de (z 憐 t ) . (z 憐 t ) et donc (z 憐 t ) . (z 憐 t ) = (z.z ) 憐 (t.t ).

Soit f : XY un morphisme de variétés irréductibles sans singularité. On définit l’image directe f : Z^m (X)Z^m+r (Y) (r = dim Y 漣 dim X); c’est une application additive telle que :

avec d = [K(W) : K(f (W))] (degré de W comme revêtement ramifié de f (W); W est un fermé irréductible de X). L’image réciproque f (t ) d’un cycle t sur Y n’est pas toujours définie; on pose f (t ) = p ((X 憐 t ). 臨^f ) où p est la projection de X 憐 Y sur X et 臨^f est le graphe de f. La codimension est conservée par f , et on a f (t ¹ + t ²) = f (t ¹) + f (t ²) et f (t.t ) = f (t ).f (t ) lorsque les deux membres sont définis. Si des cycles z et z sur X se coupent proprement, on a z.z = 嗀^X(z 憐 z ) où 嗀^X : x 料 (x , x ) est le morphisme diagonal de X dans X 憐 X. Considérons un cycle z sur X et un cycle t sur Y; on a la formule de projection f (z . f (t )) = f(z ) . t (si les deux membres sont définis).

La théorie des intersections utilise diverses notions d’équivalence de cycles (linéaire, algébrique, numérique; cf. COURBES ALGÉBRIQUES); ces relations d’équivalence sont compatibles avec l’addition des cycles et avec le produit d’intersection (et même avec les opérations f et f ). Si z et z sont des cycles quelconques sur une variété X, le produit z.z n’est pas défini en général, mais il existe un cycle z ¹ équivalent à z qui coupe proprement z ; il en résulte une loi quotient partout définie. Les propriétés (1), (2) et (3) montrent que l’ensemble des classes de cycles a une structure d’anneau commutatif .

Théorème de Riemann-Roch

Soit 杻 un faisceau cohérent sur une variété algébrique projective X sans singularité. La caractéristique d’Euler-Poincaré de 杻 est définie par :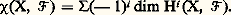

Le théorème de Riemann-Roch exprime 﨑(X, face=F0021 杻) au moyen de classes de cycles liées à 杻 et à X jouant le rôle de classes de Chern (cf. TOPOLOGIE - Topologie algébrique). Par exemple, si 硫 est un faisceau localement libre de rang 1, il s’interprète comme le faisceau des sections d’un fibré linéaire 硫; si s est une section rationnelle de 硫, on lui associe un diviseur (s ) = (s )⁰ 漣 (s ) size=1^秊, c’est-à-dire un cycle de codimension 1 sur X. On désigne par (s )⁰ l’image réciproque par s de la section nulle de 硫; (s ) size=1^秊, se construit de même à l’aide de 1/s . Lorsque X 說 P^r (k ) et que 硫 = 六^X(1) est le faisceau fondamental, (s ) est l’intersection de X avec un hyperplan de P^r (k ). Lorsque s varie, le diviseur (s ) reste dans une même classe pour l’équivalence linéaire, et cette classe D caractérise 硫 à isomorphisme près (première classe de Chern).

Si X est une courbe, le théorème de Riemann-Roch donne, pour un faisceau 硫 localement libre de rang 1 :

où deg D est le degré de la classe D, c’est-à-dire la somme des coefficients d’un diviseur quelconque appartenant à cette classe, et g est le genre de X ^{[cf. COURBES ALGÉBRIQUES]}.

Supposons maintenant que X est une surface; la formule de Riemann-Roch s’écrit :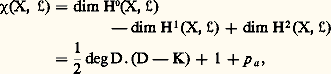

où K est une classe de diviseurs, dite canonique, et liée au faisceau des formes différentielles sur X (ou au fibré tangent à X) et où p ^a est un entier appelé genre arithmétique de X. Les invariants numériques, comme le genre arithmétique, ont été introduits initialement dans l’espoir d’arriver à une classification des variétés algébriques.

8. Groupes algébriques

On appelle groupe algébrique une variété algébrique G munie d’un morphisme m : G 憐 GG tel que pour toute variété algébrique T, l’application (u , v ) 料 m 獵 (u , v ) soit une loi de groupe sur l’ensemble G(T) des morphismes de T dans G; si T est une variété affine, d’algèbre A, on écrit souvent G(A) au lieu de G(T); par exemple si T est la variété réduite à un point avec l’algèbre k , G(T) = G(k ) s’identifie à l’ensemble des points de G (cf. chap. 2), et on voit que m définit sur cet ensemble une structure de groupe. La théorie des groupes algébriques est assez analogue à celle des groupes de Lie, mais ses méthodes sont différentes.

Comme premiers exemples de groupes algébriques, citons le groupe additif G^a , c’est-à-dire la droite affine (k , k [t ]) munie de l’addition comme loi, et le groupe multiplicatif G^m , c’est-à-dire la variété affine (k 漣0, k [t , 1/t ]) munie de la multiplication; on démontre que tout groupe algébrique affine de dimension 1 qui est connexe et réduit est isomorphe à G^a ou à G^m . L’ensemble GL(n ,k ) des matrices carrées inversibles d’ordre n est un ouvert affine dans M(n , k ) 說 Kⁿ size=1^憐n , défini par det (u ^ij ) 0; la multiplication des matrices en fait un groupe algébrique affine. Tout groupe algébrique affine s’identifie à un sous-groupe fermé d’un GL(n , k ); les groupes classiques sont des exemples de groupes algébriques (cf. GROUPES - Groupes classiques et géométrie).

On peut également définir la notion d’opérations algébriques d’un groupe algébrique sur une variété algébrique. La théorie des groupes algébriques affines, édifiée par A. Borel, repose sur le théorème suivant :

Considérons un groupe algébrique affine G résoluble et connexe , qui opère sur une variété complète X. Il existe un point de X invariant par les opérations de G.

En appliquant ce résultat à un sous-groupe algébrique résoluble et connexe de GL(n , k ) opérant sur la «variété des drapeaux» de k ⁿ , on trouve qu’un tel sous-groupe est conjugué d’un sous-groupe formé de matrices triangulaires (théorème de Lie-Kolchin ). On appelle sous-groupe de Borel d’un groupe algébrique affine G tout sous-groupe fermé résoluble connexe maximal; les sous-groupes de Borel sont conjugués par automorphismes intérieurs. Si B est un sous-groupe de Borel de G, l’espace homogène G/B est une variété algébrique projective; les sous-groupes H qui contiennent un sous-groupe de Borel (sous-groupes paraboliques) sont caractérisés par le fait que G/H est une variété complète.

À l’opposé des groupes affines se trouvent les variétés abéliennes , c’est-à-dire les groupes algébriques connexes réduits qui sont complets en tant que variétés algébriques. Si A est une variété abélienne, c’est une variété projective et sa loi de groupe est commutative. Lorsque le corps de base k est celui des nombres complexes, l’espace analytique A^an associé à une variété abélienne A est un tore complexe Cⁿ / 臨 ( 臨 sous-groupe additif discret de rang 2 n ); on peut caractériser les tores complexes qui proviennent d’une variété abélienne par l’existence d’une forme de Riemann (c’est-à-dire une forme hermitienne positive non dégénérée sur Cⁿ 憐 Cⁿ dont la partie imaginaire prend des valeurs entières sur 臨 憐 臨). Tout groupe algébrique connexe réduit G contient un sous-groupe affine connexe distingué H tel que le quotient G/H soit une variété abélienne.

À une variété algébrique complète X on associe des variétés abéliennes intéressantes: la variété de Picard et la variété d’Albanese. La première a pour ensemble sous-jacent l’ensemble des classes pour l’équivalence linéaire de diviseurs algébriquement équivalents à 0 sur X; la seconde, A, est munie d’un morphisme XA tel que tout morphisme de X dans une variété abélienne «se prolonge» à A d’une manière unique. Si X est une courbe, la variété de Picard et la variété d’Albanese coïncident, et portent le nom de jacobienne de X; la dimension de la jacobienne est égale au genre de X.

● Géométrie algébrique branche de l'algèbre issue de l'étude des courbes algébriques du plan R² ou de l'espace R³ et des surfaces algébriques de l'espace R³.

Encyclopédie Universelle. 2012.